Kolize hashovacích funkci a narozeninový paradox (25. díl)

20. Zář. 2007

Kolize hashovacích funkci a narozeninový paradox (25. díl)

V minulých dílech seriálu jsme se několikrát setkali s pojmem narozeninový paradox.

Pojďme si nyní tento pojem na jednoduchém příkladu přiblížit.

Mezi dvěma typy kolizí popsanými v minulých dílech našeho seriálu je zásadní rozdíl, který bývá popisován jako „narozeninový paradox„.

Položme si jednoduchou otázku: jestliže budeme mít množinu náhodných dokumentů, jak bude muset být tato množina velká, aby v ní s nezanedbatelnou pravděpodobností existovali dva různé dokumenty se stejným otiskem?

Pomožme si opět jednoduchým příkladem: pokud se sejde určitý počet lidí, jaká je pravděpodobnost, že dva z nich mají narozeniny ve stejný den? Vezměme v potaz tyto předpoklady:

rok má dejme tomu 365 dní*
uvažujeme teoretickou (statistickou) pravděpodobnost – tedy nikoliv dvojčata, srazy šedesátníků, atd.
hledáme shodu narozenin nikoliv stejných narozenin (tedy shodného data narození nikoliv data i roku)
nikdo nemá narozeniny 29. února

*Jak dlouhý je vlastně rok? Rok je doba, která uběhne mezi dvěma opakováními události spojené s oběhem Země kolem Slunce.

Siderický rok – doba, za kterou oběhne Země kolem Slunce vzhledem ke vzdáleným hvězdám. Trvá 365 dní, 6 hodin, 9 minut a 9 sekund.

Tropický rok – doba mezi dvěma průchdy Slunce jarním bodem. Trvá (365 dní, 5 hodin, 48 minut a 45 sekund. Je to taky perioda se kterou se střídají roční období a jeho délka je tedy důležitá pro tvorbu kalendáře.

Anomalistický rok – doba, která uplyne mezi dvěma průchody Země přísluním (perihéliem). Trvá 365 dní, 6 hodin, 13 minut a 52 sekund. (zdroj: http://cs.wikipedia.org/wiki/Rok)

Pokud bychom hledali takovéto dva lidi, pak bude záležet také na tom, jestli budeme hledat jakékoliv (libovolné) dva lidi, kteří mají narozeniny ve stejný den, nebo jestli budeme hledat ke konkrétnímu člověku druhého, který má narozeniny ve stejný den.

Tyto dva pohledy jsou právě rozdílem mezi kolizí prvního řádu (libovolní dva lidé) a kolizí druhého řádu (nalezení druhého člověka k danému). (zdroj: časopis Crypto-word 4/2005 – Klíma, Vlastimil: Co se stalo s hashovacími funkcemi.)

Nalezení jakékoliv osoby:

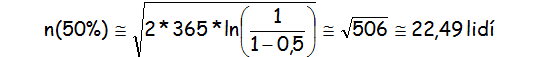
Nalezení konkrétní osoby:

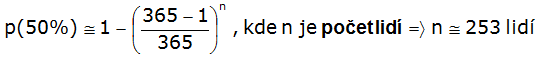
Pokud bychom se spokojili s padesátiprocentní pravděpodobností pak pro shodu narozenin dvou libovolných lidí nám bude stačit 23 lidí. Zatímco pro nalezení člověka se stejným konkrétním datem narození jich bude třeba více – 253.

Graficky by bylo možné zobrazit průběh funkcí takto:

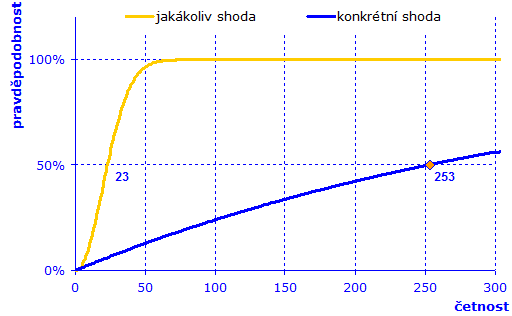
Narozeninový paradox

Závěr tohoto jednoduchého příkladu má v kryptologii velký význam. Při pokusech o prolomení funkce a nalezení dokumentu se stejným otiskem. Útoky hrubou silou jsou v případech použitelnosti narozeninového paradoxu totiž mnohem snazší a říká se jim pak narozeninový útok.

Jestliže použijeme n-bitovou hashovací funkci pak by měla nastat kolize s pravděpodobností 50% v množině 2^n/2 dokumentů namísto očekávaných 0,5*2^n. Například pro 256 bitový hašový kód bychom očekávali 0,5*2^256 dokumentů, paradoxně je to pouhých 2^128 dokumentů. Kromě „kvality“ použité funkce tedy záleží i na její délce.

n	2^n/2	2^n/2	(2^n)/2	( 2^n)/2
32	216	65 * 10^3	(2^32)/2	2,1 * 10^9
64	232	4,2 * 10^9	( 2^64)/2	9,2 * 10^18
128	264	18 * 10^18	(2^128)/2	170 * 10^36
256	2128	340 * 10^36	(2^256)/2	58 * 10^75
512	2256	115 * 10^75	(2^512)/2	6,7 * 10^153

Rozdíl mezi kolizí prvního a druhého řádu (výpočtené hodnoty jsou zaokrouhlené)

Z tabulky je zřejmé, že rozdíl mezi kolizí prvního a druhého řádu je podstatný rozdíl, ale při použití 256 bitové a vyšší funkce je použití přiměřeně bezpečné.

Díly seriálu:

Elektronický doklad v účetnictví – Podpis (1. díl)

Elektronický doklad v účetnictví – Vlastnoruční podpis (2. díl)

Elektronický doklad v účetnictví – Elektronický podpis (3. díl)

Požadavky kladené na elektronický podpis (4. díl)

Druhy elektronických podpisů (5. díl)

Doklad v účetnictví (6. díl)

Náležitosti účetního dokladu (7. díl)

Co vše skrývá dokument v elektronické podobě (8. díl)

Elektronický podpis a informace v něm obsažené (9. díl)

Elektronická komunikace organizace (10. díl)

Možnosti elektronické komunikace organizace (11. díl)

Efektivní elektronická komunikace – to je EDI (12. díl)

EDI a ti druzí (13. díl)

Šifrování – kryptografické základy digitálního podpisu (14. díl)

Význam šifrování a jeho typy (15. díl)

Symetrické šifrovací algoritmy (16. díl)

Šifrování – k čemu slouží a jak ho využít (17. díl)

Ověření identity a elektronický podpis (18. díl)

Asymetrické šifrování a jeho praktické využití (19. díl)

Hybridní šifrovací algoritmy (20. díl)

Hashovací funkce a jejich využití ve spojení s elektronickým podpisem (21. díl)

Vlastnosti hashovacích funkcí (22. díl)

Použitelnost hashovacích funkcí v praxi (23. díl)

Elektronický podpis – využití certifikátu (24. díl)

Kolize hashovacích funkci a narozeninový paradox (25. díl)

Certifikát elektronického podpisu – co ještě potřebujete vědět (26. díl)