Vlastnosti hashovacích funkcí (22. díl)
V minulém díle seriálu jsme se krátce seznámili s takzvaným otiskem neboli hash funkcí.
Dnes se podrobněji zaměříme na její základní vlastnosti a na jejich konstrukci.
Od kvalitní hash funkce očekáváme následující základní vlastnosti:
Jednosměrnost
Jednosměrnost nebo také jednocestnost, irreversibilita, preimage resistance – pro každé x je možné jednoduše vypočítat f(x) (hodnota hash funkce musí být jednoduše vypočitatelná pro jakýkoli vstupní řetězec, z otisku nelze odvodit, alespoň ne v časově omezeném úseku (Výpočet je sice teoreticky možný, ale při současných omezeních výpočetní techniky by i při spojení velkého množství výkonných počítačů trval takový výpočet řádově desetiletí.
Vzhledem k tomu, že certifikáty ke kvalifikovaným elektronickým podpisům jsou zpravidla vydávány s platností omezenou na rok či dva je zneužití takového výpočtu velice nepravděpodobné.), původní dokument. Dokonce ani neumíme (v rozumném čase) najít k danému otisku nějaký text, který by měl právě tento otisk.)
Zdroj: volně dle materiálů Společnosti pro informační společnost – Konference „Elektronická fakturace“, která proběhla 26. 11. 2003 v Kaiserštejnském paláci.
- pro náhodně zvolené x je výpočetně velmi náročné z f(x) určit x
- využití například při ukládání hesel
Obrázek 1: Jednocestnost hash funkce
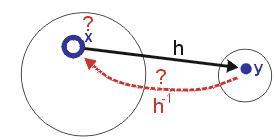
Odolnost proti kolizi prvního řádu
– odolnost proti kolizi prvního řádu (collision resistance) – rozdíly mezi kolizemi si vysvětlíme později v některém z dalších dílů seriálu na příkladu narozeninového paradoxu.
– je výpočetně velmi náročné nalézt libovolné různé x, y tak, že h(x) = h(y), složitost nalezení kolize je přibližně 2^n/2
– funkce je silně bezkolizní, pokud není výpočetně možné najít dva různé texty se stejným otiskem
Obrázek 2: Silná odolnost proti kolizím
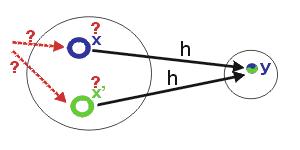
Odolnost proti kolizi druhého řádu
odolnost proti kolizi druhého řádu (second preimage resistance)
– je výpočetně velmi náročné k danému náhodnému x nalézt druhý vzor y různý od x tak, že h(x) = h(y), složitost nalezení kolize je přibližně 2^n
– funkce je slabě bezkolizní, pokud k danému textu není výpočetně možné vymyslet jiný text, který bude mít stejný otisk.
– využití v digitálních / elektronických podpisech
Obrázek 3: Slabá odolnost proti kolizím
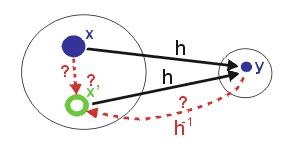
- vstup může být jakékoli libovolné délky (velikost souboru závisí spíše na omezeních operačního systému)
- výstup musí mít pevnou délku (v rámci určité hash funkce) – převzato a upraveno dle abclinuxu.cz a wikipedia.org.
Pokud se vrátíme k obraznému srovnání s člověkem a jeho otiskem prstu naznačeném v minulém dílu seriálu, pak zatímco podle otisku prstu jsme schopni ukázat na člověka, kterému patří, ale nejsme schopni podle otisku prstu zrekonstruovat kompletní popis člověka, kterému patří. Stejně tak je velmi těžké najít dvě osoby se stejným otiskem prstu a ještě těžší nalézt druhou osobu se stejným otiskem prstu jako určitá daná osoba.
pozn: Obrázky převzaty z: Kment, Vojtěch: Hašovací funkce: Jak se odolává hackerům, www.lupa.cz
Díly seriálu:
Elektronický doklad v účetnictví – Podpis (1. díl)
Elektronický doklad v účetnictví – Vlastnoruční podpis (2. díl)
Elektronický doklad v účetnictví – Elektronický podpis (3. díl)
Požadavky kladené na elektronický podpis (4. díl)
Druhy elektronických podpisů (5. díl)
Náležitosti účetního dokladu (7. díl)
Co vše skrývá dokument v elektronické podobě (8. díl)
Elektronický podpis a informace v něm obsažené (9. díl)
Elektronická komunikace organizace (10. díl)
Možnosti elektronické komunikace organizace (11. díl)
Efektivní elektronická komunikace – to je EDI (12. díl)
Šifrování – kryptografické základy digitálního podpisu (14. díl)
Význam šifrování a jeho typy (15. díl)
Symetrické šifrovací algoritmy (16. díl)
Šifrování – k čemu slouží a jak ho využít (17. díl)
Ověření identity a elektronický podpis (18. díl)
Asymetrické šifrování a jeho praktické využití (19. díl)
Hybridní šifrovací algoritmy (20. díl)
Hashovací funkce a jejich využití ve spojení s elektronickým podpisem (21. díl)
Vlastnosti hashovacích funkcí (22. díl)
Zdroje:
[1] cryptography.hyperlink.cz
Osobní stránky Dr. Vlastimila Klímy[2] crypto-world.info
Crypto-World[3] www.lupa.cz
server o českém Internetu, ISSN 1213-0702[4] VONDRUŠKA, Pavel: Cesta kryptologie do nového tisíciletí. Computerworld 37/2000.
[5] www.abclinuxu.cz
ABC Linuxu, ISSN 1214-1267















Odpovědět na příspěvek